日記：2024年5月
1日 (水)
午前に強制法入門セミナーをした。後輩の発表を聞いたが、しっかりと発表していた。 午後、F先生による集合論セミナーをきいた。
研究室の様子。
2日 (木)
松山に旅行に行く。懐かしい。
愛媛大学理学部に寄ったら、おしゃれな自習スペースができていて驚いた。
とあるけみすと、三河くん、ほとんどいたるところ微分可能ななにかさんと飲み会をした。3次会まで行って楽しかった。
3日 (金)
するがビバップと昼食を食べ、同じカフェでするがビバップと藤田先生といろいろ喋る。 その後、するがビバップの働いているスペイン料理屋に行った。
4日 (土)
松山駅近くのカフェでKamo-Osugaの論文を読んだ。
松山から神戸に帰った。良い旅行だった。
瀬戸大橋からの眺め。
5日 (日)
特に書くことなし。
6日 (月)
ポモドーロ・テクニックで25分勉強+5分休憩を2セットした。
7日 (火)
久々にハリーポッターのディクテーションをした。
消化器科に行った後、プールに行った。400m泳いだ。
8日 (水)
午前、強制法セミナー。Delta 0絶対性のことを話した。
Kobe Set Theory SeminarでHausdorff測度について話した。英語発表はやっぱりかなりつかれる。
9日 (木)
IELTSのリーディングの問題を1問解いた。これから毎日やっていこうと思う。帰ってからSwitchの英検対策ソフトもやった。
10日 (金)
Howroydの定理の理解に向けて、定理2つと補題1つの証明を読んだ。
実家に帰宅した。
11日 (土)
クリニックの待ち時間でKunenのSet Theoryの0章を読んだ。
Howroydの定理の理解に向けて、命題を一つ読んだ。
『志学 数学』を読み終えた。数学の研究をする上で参考になること (机の上で考えるだけでなく歩いて考えることが大事だとか、数学以外の文学などにも触れるとよいとか)が書いてあってためになった。
『ここで差がつく！英文ライティングの技術』をちょっと読んだ。"S V, so S can V"のような文を連発すると単調になるのでenableみたいな動詞をうまく使うという話が参考になった。
つどいの会議をした。
12日 (日)
今やっていることにドンピシャな補題を偶然見つけ、一つ新しいことを示せた。
13日 (月)
PawlikowskiのLaverモデルがouter measureを保存する証明を読んで理解した。
しかし、この証明で使われているランダム強制法の性質は本質的なのかが気になる…。
14日 (火)
嬉しいお知らせが届く。
15日 (水)
分離できないはずの基数不変量が分離できたので、今日もZFCが矛盾した…と思った15分後、間違いに気づいた。
16日 (木)
本を買った。
最寄りのコンビニ (20数分先)まで歩いて、買い物して、食べ歩きしながら帰ってきた。
17日 (金)
学振の申請書草稿を同僚に見てもらって、たくさんコメントを頂いた。ありがたいことである。
ジェネリック実数の擬人化をらくがき。
18日 (土)
プールで泳いだ。400m。
19日 (日)
日記：2024年4月後半
15日 (月)
某申請書の締め切りだった。最近これのために数学がなかなかできず、神経がすり減っていた。 明日から数学再開していく。がんばるぞ～
16日 (火)
午前中久しぶりの数学をした。不等式ゴリゴリの補題の証明を追った。楽しかった。 昼前に健康診断を受けた。東京に移動した友人とzoomミーティングした。 帰りの電車で志学数学とInfinite-Dimensional Topologyを少し読んでモチベが上がった！
17日 (水)
昨日に引き続きとある論文を読み進める。かなり重たい感じの補題を一つ読んだ。 神戸集合論セミナーを聴く。densityに関する基数不変量の話で面白い内容だった。
18日 (木)
朝8時からある映画を見ようかなと思っていたが、結局11時くらいまで二度寝して見れず。 引き続きとある論文を読み進める。補題を2つ読んだ。
19日 (金)
某論文を読み進めた。 強制法入門テキストを書き進めた。 研究報告書が締め切り明日なのに書いてなかったので急いで書いて出した！ 研究室の歓迎会を楽しんだ (実際は歓迎回の後に数人で見たイナズマイレブンの方が記憶に残ってしまっている)
20日 (土)
昨日の酒のせいでずっと寝ていた。
21日 (日)
同僚の研究の手伝いで久しぶりにプログラミングをした。
22日 (月)
映画ゴジラ-1.0を見に行った。面白くて、良い気分転換になった。
23日 (火)
K先生のセミナーをきいた。ロジックにそこまで慣れてない人もきくことを想定して丁寧に説明していたのでかなりわかりやすかったし、面白かった。
24日 (水)
強制法入門セミナー第1回を担当した。算術をやっている後輩2人に強制法を最短コースで教えるセミナーである。
午後から先生とミーティングした。そのあとF先生による集合論のセミナーを聴いた。
25日 (木)
久しぶりに自分の研究に集中して取り組める時間が取れた。よいことだ。
昼間は学生部屋で証明できるとは何なのかといった話題で持ち切りだった。そこで証明可能性術語をカレーに例えてた議論が聞こえてきて食べたくなったので、インドカレー屋に行き、食べた。
夜、AtCoderとマイナビの就職活動準備のzoomセミナーをきいた。結構面白かった。
↑昼間、疲れていたので北側のキャンパスまで散歩した。そのときの写真
26日 (金)
学生部屋で「研究室以外に何か属しているコミュニティを持つのは大事だよね～」という話をした。
27日 (土)
「映画ドラえもん のび太の地球交響楽」を見た。良い話で泣いた。
研究をちょっと進められた。よいこと！
28日 (日)
プールで500m泳いだ。
研究室で同僚にちょっと痛むことを言われてしまった (当たっている指摘だから痛むのだけど)。
29日 (月)
相変わらず、お休みだけど大学に来る。
FremlinのMeasure Theoryを一部読んだ。Howroydの定理の証明を知るためのRadon測度の定義を知るためにlocally determinedの定義を見た。
30日 (火)
久々に自分で何か新しく示せたかも、と思ったが証明に間違いがあった。
日記：2024年1月中旬
1月13日(土)
共通テストのため大学にこの週末は大学に入れない。 6時からつどいの会議なので5時40分にアラームを設定して安心して作業をしていたら、午前の5時40分に設定していたので遅刻した。すいません
1月14日(日)
藤田『ホワイトヘッドの問題について』第7節を読んだ。MA_{aleph_1}を仮定すればサイズaleph_1のWhitehead群だが自由群でないものが存在することの証明を追った。 これで一通りこの文献は読み終わった。短い文献はちゃんと読み終わらせることができてよい。
1月15日(月)
海外の学会の参加のため、参加費を銀行で送金。そのための住所変更のための住民票の写しをもらう手続きがあって疲れた。 神戸集合論学生セミナーに参加。位相と様相論理の話、面白そうだなあと思った。 今日は実家に帰った。
1月16日(火)
疲れていて何もできず。
1月17日(水)
区役所に行って自立支援の延長を行った。えらい。 チェコに行くためのレンタルポケットWi-Fiやホテルの予約などをした。 チェコの研究集会のスライド (10日後開始)のスライドをようやく作り始めた。
1月18日(木)
指導教員とミーティングした。cccのfsiで今考えている原理を強制できるかということを議論した。 Whitehead群のセミナー第3回だった。
1月19日(金)
海外に行くための事務仕事をいくつかした。 cccのfsiでぱっと思いつく候補では今考えている原理を強制できないことがわかった。 前から読もうと思っていたBorel conjecture and dual Borel Conjectureを読み始めることにした。
日記：2024年1月上旬
2024年は日記をつけていこうと思います。
おまけ(?)で12月30日と31日の日記も書いちゃいます。
2023年12月30日(土)
最近読んでいる藤田の『ホワイトヘッドの問題』。今日はサイゼリヤで第3節を読み終えた。 特に、特に(B, Z)群の話とシュタインの定理(可算なホワイトヘッド群は自由)を読んだ。 まだ消化不足かも。
夕方からすうがく徒のつどいの会議。人をleadする経験があまりないので意思決定など難しい。 しかし、運営の人々が活発に動いてくれて、良い会になりそう。
夜に『プログラミングRust』の第4章『所有権と移動』を読んだ。
2023年12月31日(日)
親に帰ってきたら、と言われたので、帰省した。といっても同じ市内である。
電波通信の「ウリソーン普遍空間の構成」という記事を読み始める。
3節のKatětov写像に関する部分を3割ぐらい読んだ。Katětov写像の概念がいきなり登場してなんじゃこりゃとなるが、徐々に重要性がわかってくるのが面白い。
2024年1月1日(月)
実家には1日しか留まらず、アパートに戻ってきた。親がいろいろと食べ物などを持たせてくれた。
夜に『プログラミングRust』の第5章「参照」を読んだ。 プログラマの代わりにコンパイラがチェックする思想は良いと思った。理論的背景には線形型システムというものがあるそうだが、そこまでは解説してくれないので、だいたいこういう感じでコンパイラがちゃんと悪いコードをチェックしてくれますよーということは学べた。
4章の最後によると『所有権と借用を理解すれば、Rustの学習曲線の最も急な部分を登り終えたことになり、Rustの特徴を利用する準備ができたことになる。』そうである。
2024年1月2日(火)
体調悪めだった。 家で焼肉を食べた。サラダ油がなかったので、バターで焼いた。 『プログラミングRust』第6章「式」を読んだ。 とあるゲームの解析に夢中になってしまって、午前4時くらいまで起きていた。
2024年1月3日(水)
『プログラミングRust』第7章「エラー処理」と第8章「クレートとモジュール」を読んだ。 『ホワイトヘッドの問題』に関して、さらっと書いてあって、まあ出来るんだろうなとこの前は自分でも流した事実があるのだが、ちゃんと確かめようとしたら結構苦戦……。
IELTSの登録をしたので、英語学習のモチベーションが生まれた。久しぶりにSwitchの英検対策ソフトをしっかりやったり、ポッドキャストを聴いたりした。
2024年1月4日(木)
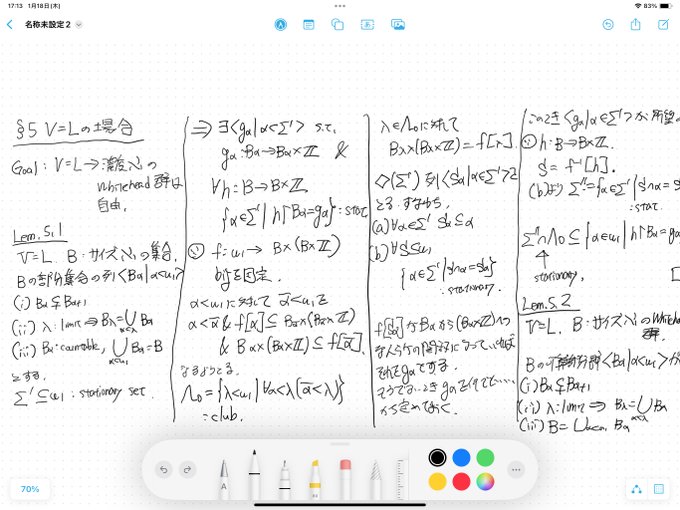
久しぶりに大学に登校！ しかし、大学内のコンビニも学食も閉まっていたので、研究室の冷蔵庫に残っているものでお昼ごはんを食べた。 午後からホワイトヘッド群の自主セミナー第1回。
1個分からない行間が残って宿題となった。
2024年1月5日(金)
午前に新年最初の指導教員とのミーティング。数学の話のほか、卒業後の進路の話もした。
今日は午後に胃カメラを撮る予定で朝からの絶食をがんばったのに、1ヶ月以内に熱を出したからというので撮ってもらえなかった。悲しい。
ホワイトヘッド群の分からなかった行間を埋めることができた。
2024年1月6日(土)
すうがく徒のつどいのwebサイトの引き継ぎを行った。 夕方からゲームのハックに夢中になってしまって、今日は数学をできなかった。
2024年1月7日(日)
しんどくて何もできず。
2024年1月8日(月)
すうがく徒のつどいの歴史ページをつくった。
2024年1月9日(火)
ここ最近風邪みたいな症状が長続きするので、内科に行った。
2024年1月10日(水)
ゲームのハックに夢中で徹夜してしまった。
2024年1月11日(木)
午前はWhitehead群のセミナーをした。3節の最後の定理を僕が発表し、4節の内容をサクラさんが発表してくれた。久しぶりに数学ができて感覚を取り戻せた。 午後には指導教員とのミーティングもあった。 研究に関して「今まで考えてた方針だと無理」とわかって「では逆にこういうのが成り立つのでは？」という予想が立って楽しい。
2023年振り返り
振り返り
1月〜3月からはカナダのトロントに行っていた。後半あまり体調よくなかったけど、全体的には友達もできたし色々学べたのでよかったと思う。
今年新しくプレプリントを出した論文は以下：
今年アクセプトをもらった論文の数は0。悲しい。
この論文について、数学基礎論若手による会 (東京・9月)、日本数学会 (東北・9月)、RIMS (京都・10月)、Asian Logic Conference (中国・10月)で話した。さすがに同じネタで話しすぎて飽きた。
9月に第4回すうがく徒のつどい@オンラインも開催したのであった。9月10月はイベント多すぎで馬鹿みたいに忙しかった。
10月に1週間くらいAsian Logic Conferenceのために中国の天津に行っていた。 こちらも同じく途中から体調を崩してしまった。 ホテルは毎朝豪華なバイキングの朝食が出るし、部屋が1人用の個室なのにバカでかいのが印象的であった。
12月には数学基礎論若手の会に参加するために千葉にも行った。数年ぶりの若手の会はとても楽しかった。
今年は絵を4枚書いた。pixivで見てね！
9月26日から不定期的に後輩のHくんとElementary Embeddings and Algebraのセミナーもしている。今第6回まで行った。
来年やりたいこと
心身に気をつけて色々チャレンジしたい。博論に向けて研究を収斂させていきたい。
余談
はてなブログにAIに記事タイトルをつけてもらう機能がついていたので試した。
神戸大付近のごはん屋
この記事は、ましょさんが企画なさった、「数学徒が紹介するおいしいごはん Advent Calendar 2023」の2日目の記事です。
神戸大学付近のおいしいごはん屋さんを紹介します。
まず述べなければならないのは、神戸大学付近には生協食堂以外全然お店がないということです。ある程度大学から降りれば色々店があります。
神戸大学の生協食堂
大学から近く比較的安価に食べれます。画像には載せているものと別ですが、油淋鶏などの揚げた鶏の系統の食事は結構おいしいです。
pizzeria romana IL VENTO da REMO
(画像なし)
釜で焼き立てのおいしいピザが食べれるお店です。大学から一番近いごはん屋かも？ お店のキャパは大きくないので、特にディナーは、予約していくのが良いと思います。
扇屋
大学からそこまで降りずにたどり着けるごはん屋さんです。うどん・そば・丼ぶりなどを提供しています。比較的気軽に行けていいと思います。
山猫軒
ここらは大学からある程度降りなければならないところです。山猫軒は洋食屋さんです。値段帯は1000円〜2000円ぐらいと学生には若干値段がはるところですが、おいしい洋食が食べられます。
RYU-RYU
阪急六甲駅にあるお店です。値段帯は2000円〜3000円ぐらいでちょっと良い食事をしたいときに選ぶといいでしょう。前菜やデザートもついたいい感じのイタリアンの食事が食べられます。
しゅはり
ラーメンやまぜそばなどを提供しているお店です。JR六甲道駅を少し超えたあたりにあります。私の後輩は「食べると脳がバグる」と絶賛していました。
六甲道駅付近にはほかにも色々麺屋さんがあり、どうやら激戦区のようですね (特に、鶏ぱいたん系が多い印象があります)。色々試してみてください。
まとめ
大学〜阪急六甲駅まではお店が少なめですが、それを超えるとたくさんお店があるので、皆さんも色々開拓してみるといいと思います！
Schemeで非決定性を使った、トランプから取り出した2枚が両方とも赤のカードである確率を求めるプログラム
Schemeで非決定性を使い、シャッフルされた、ジョーカーを除いたトランプ(52枚)から2枚同時に取り出してそれが両方とも赤のカードである確率を求めるプログラムを書いてみました。
マクロamb、マクロset-of、関数assertはScheme 入門 18. 非決定性によるものです。
(define fail #f) (define-syntax amb (syntax-rules () ((_) (fail)) ((_ a) a) ((_ a b ...) (let ((fail0 fail)) (call/cc (lambda (cc) (set! fail (lambda () (set! fail fail0) (cc (amb b ...)))) (cc a))))))) (define-syntax set-of (syntax-rules () ((_ s) (let ((acc '())) (amb (let ((v s)) (set! acc (cons v acc)) (fail)) (reverse acc)))))) (define (assert pred) (or pred (amb))) (define (remove-value lst val) (remove (lambda (x) (eq? val x)) lst)) (define (element-in list) (let loop ((xs list)) (if (null? xs) (amb) (amb (car xs) (loop (cdr xs)))))) (define all_cards (iota 52)) (define (red? card) (= (remainder card 2) 0)) (define (black? card) (= (remainder card 2) 1)) (define (choose-two-cards) (let* ((card1 (element-in all_cards)) (card2 (element-in (remove-value all_cards card1)))) (cons card1 card2))) (define (redred) (let* ((card1 (element-in all_cards)) (card2 (element-in (remove-value all_cards card1)))) (assert (red? card1)) (assert (red? card2)) (cons card1 card2))) (print (/ (length (set-of (redred))) (length (set-of (choose-two-cards))))) ;; 25 / 102
所望の確率は、ちょっとレシートの裏に計算すれば一般のnに対して求まるんですが、それはご容赦を。
ていうか本当に求めたかったのはシャッフルされた札から2枚ずつカードを引いて、赤と赤の組、赤と黒(順序不同)の組、黒と黒の組にそれぞれ分けて山を作ったとき、それぞれの山の中のカードの数の期待値だったんですが、それを非決定性を使ったプログラムで求めるのは厳しそうだったので断念。
