2017-04-03

CのサブセットをJSで実装した

f:id:fujidig:20170403225601p:plain

CのサブセットをJavaScriptで実装しました。

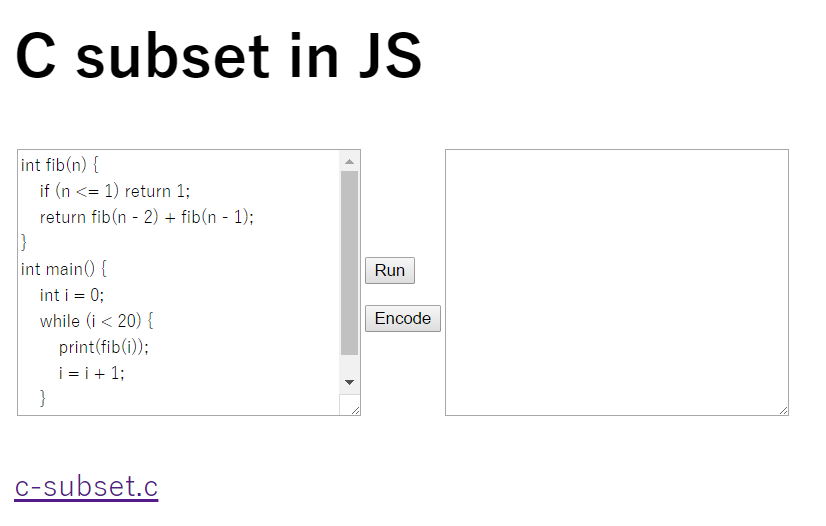
以下のページで動かせます。

https://fujidig.github.io/c-subset-in-js/

ソースコードは以下

https://github.com/fujidig/c-subset-in-js

実装している機能は以下の通り。

型は多倍長整数型のみ (それをintと書いている)
変数代入、参照
各種演算子
if, else, while
関数呼び出し, return

たとえば

int fib(n) {
    if (n <= 1) return 1;
    return fib(n - 2) + fib(n - 1);
}
int main() {
    int i = 0;
    while (i < 20) {
        print(fib(i));
        i = i + 1;
    }
}

を実行すると次を得ます。

整数型が多倍長であるため次のようなプログラムを動かすと簡単に2の1000乗を出力できます。

int main() {
    print(1 << 1000);
}

10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376

また、コードを自然数に符号化する機能を搭載しています。

さらにCのサブセット自身で実装したCのサブセットのインタプリタがついています。

これにより、Cのサブセット in 「Cのサブセット in JS」ができます。

やってみましょう。

int main() {
    int a = 233, b = 377, c;
    int n = 1;
    while (n <= 5) {
        c = a + b;
        a = b;
        b  = c;
        print(c);
        n = n + 1;
    }
}

再帰フィボナッチは遅いので変更しました。また、フィボナッチ数の途中から5項を表示するよう変更しました。

これを実行すると

が得られます。

実行する代わりにEncodeボタンを押すと

2151370312757585239013893921680792355662486752412569148118764178423124275394560545515699620618390679749954365463276712440703239868128831904427466606016571762297213794979160614374073563745430656004482516317773057589341025004447961146147390127286244343288796934705377531463089162718506253985211455134666431223509512551974414474343672462798521790265803007504943944452569884958093931851114825905529277320800919509394108815581895937704399123986982191200330618144264490236450820715210311575386269331510535250444367316207434769401257253036824832178335578381245463684416737106182236342817759700301368800684649996332165657549447346233743185772934210938808280331980784115355655494351600163821670576622405334837112429337898494085760016249953010029070098290452099149093585994645858969474021323699095659397804178564149616100171888900802875821501165465628689469074724933056047927805153388198042811328724820317873906070961308820216848154752868246705991047232511137406181737589847980927438034993293142569425322534863372670621084881997309475592027063848468052474819497979418075183190689400892317362249982654264328698779198933832859573184531758281526678767231853049237813637063306722059557355922220218076338507472883800169331749000288864555086756341752671027190130207526809765937180

が得られます。

これをc-subset.cのmain関数内のevalの第一引数に指定します。

int main() {
    return eval(2151370312757585239013893921680792355662486752412569148118764178423124275394560545515699620618390679749954365463276712440703239868128831904427466606016571762297213794979160614374073563745430656004482516317773057589341025004447961146147390127286244343288796934705377531463089162718506253985211455134666431223509512551974414474343672462798521790265803007504943944452569884958093931851114825905529277320800919509394108815581895937704399123986982191200330618144264490236450820715210311575386269331510535250444367316207434769401257253036824832178335578381245463684416737106182236342817759700301368800684649996332165657549447346233743185772934210938808280331980784115355655494351600163821670576622405334837112429337898494085760016249953010029070098290452099149093585994645858969474021323699095659397804178564149616100171888900802875821501165465628689469074724933056047927805153388198042811328724820317873906070961308820216848154752868246705991047232511137406181737589847980927438034993293142569425322534863372670621084881997309475592027063848468052474819497979418075183190689400892317362249982654264328698779198933832859573184531758281526678767231853049237813637063306722059557355922220218076338507472883800169331749000288864555086756341752671027190130207526809765937180
, 0, 0);
}

int eval(int code, int nodeid, int vars) {
    int type = node_type(code, nodeid);
....

これを実行すると

が得られます。Cのサブセット in 「Cのサブセット in JS」ができました！

さて、Cのサブセット in 「Cのサブセット in JS」ができたらCのサブセット in 「Cのサブセット in 「Cのサブセット in JS」」もできそうですね。

出来ます。

上のコードをエンコードすると

5980329765610774127525245562340339041698066219641944319743934783175611745424082081909469512081526404990329327307663133360222179842204167878590696763364369328310595163512492390306181732744829222117518824617582650725740141952748499132995210154143453650196442366092313540868501218530765785202077459350045124230485161555127015535579281731237549416807088489950668251201877691301786506164869080335350936836780724474957976693965274738312936528413281682587340098367064230914323095122080804227660640366503916932207643381263729480625878251063342344491321746310705742164611935632444361598814398154552165339705969745088135940227990524875871445306557373704956903790714486847060660398146659416808412916342257564327042373789893508885075423093377342769000461009027832643305332470849028124039319790277321370911576608973742123713974755184012440142143498846118718870205865840232155186970509391712672169731177405233(中略)510598683619980655730447704072561755011557496861802213363042657146272152051448253232537222993284478241218521508753627807397667295345210321588828661028882576723361390442917570826740418840091727961426165295412166642922565427783394382300102978854750486841360479884360285646613836830334791874344769258423639706904789757288203770209076874980661725022227457454699592036668175729583056522607392923069630915743528982026403631785420924844469140930747327055844004757819140600689335892552518129228445853661349397832112260734508951124297567328771727350631899147423428097500075927570655026017406849604335337201966560953461194685273199307383470572710728285812162887665935977834511174577930840561717165020285218028369094475113108152679840829208807917849465770186516199998023505234400192250998515347296598256278102675603598662702878579009777455897033506640154580988505799442586296556106438320022128549948147421815478517853957228970488937248269631079685300035177024830468421766270037213040053707234917678845100597776938552755275192861496

という37957桁の自然数が得られます。これをc-subset.cのmain関数内のeval呼び出し部分に入れて実行してみましょう。

時間がかかります。

f:id:fujidig:20170403232236p:plain

ブラウザがこのようなアラートを出すほど時間がかかりますが待ちましょう。

結果、次の出力が得られます。

Cのサブセット in 「Cのサブセット in 「Cのサブセット in JS」」が出来ました！私の環境だと実行を終えるのに61秒かかりました。たくさん時間がかかるとはいえ、間違いなく実現できています。よかったですね。

2016-04-01

不定形の極限であって収束するが，ロピタルの定理を使っては極限値を求められない例

$$ \lim_{x \to 0} \frac{\int_{t=0}^x \sin (1/t) dt}{x} $$ は不定形の極限($0/0$型)であり，この極限は$0$に収束する．一方で分母分子をそれぞれ$x$で微分したものの極限 $$ \lim_{x \to 0} \sin (1/x) $$ は発散する．よって最初の極限の値はロピタルの定理を使っては求められない．

2016-02-05

XorShiftの一例が周期最長になることを確かめるPari/GPプログラム

XorShiftと呼ばれる疑似乱数のうち状態ベクトルが64ビットである例を一つとり、これが最長の周期2^64-1を達することを確認する。

\\ determine that order of g equals to n
isprimitive(g, n, e=1) = {
  my(factors, p);
  if (g^n != e, return(0));
  factors = factor(n);
  for (i = 1, matsize(factors)[1],
    p = factors[i, 1];
    if (g^(n/p) == e, return(0)));
  return(1);
}
\\ identity matrix
E = matid;
\\ right & left shift matrix
R(n, k) = { return(matrix(n, n, i, j, i + k == j)); }
L(n, k) = { return(R(n, -k)); }
\\ convert to matrix on F_2
to_f2(mat) = { return(matrix(matsize(mat)[1], matsize(mat)[2], i, j, Mod(mat[i, j], 2))); }

n = 64;
T = to_f2((E(n) + L(n, 17)) * (E(n) + R(n, 7)) * (E(n) + L(n, 13)));
print(isprimitive(Mod(x, charpoly(T, x)), 2^n - 1));

参考:

2015-12-14

自然数の定義

順序数

以下の条件を満たす集合$x$を順序数と呼ぶ。

$x$のどんな要素も$x$の部分集合である
$x$は属する($\in$)という関係において整列順序集合である

順序数の間には属するという関係で全順序が定まる。そこで順序数$\alpha, \beta$に対して$\alpha \in \beta$のことを$\alpha < \beta$と書く。

0

空集合$\{\}$は順序数である。そこでこれを$0$と書く。

後続数

順序数$\alpha$に対して $$ S(\alpha) = \alpha \cup \{\alpha\} $$ を$\alpha$の後続数という。

後続順序数

順序数$\alpha$に対して、$\alpha = S(\beta)$となるような順序数$\beta$が存在するとき$\alpha$を後続順序数という。

自然数

順序数$\alpha$は、$\alpha$以下の任意の順序数$\beta \ne 0$が後続順序数であるとき自然数と呼ぶ。

参考文献

Kenneth Kunen (1980) Set Theory - An introduction to independence proofs, North Holland

自然数とは有限の順序数である、という定義だと有限集合の定義と循環してしまうよなーと思って調べました。

自然数とは$\omega$より小さい順序数である、$\omega$とは($0$を除いて)最小の極限順序数である、という定義でもよさそうですね。

2015-08-30

一次分数変換を試すプログラム

猫画像版: http://fujidig.github.io/fractional-transform/
市松模様版: http://fujidig.github.io/fractional-transform/#checker

f:id:fujidig:20150830162334j:plain

f:id:fujidig:20150830162528p:plain

複素平面上の変換$z \to \frac{z - \alpha}{z - \beta}$を試すプログラムです。赤丸が$\alpha$, 青丸が$\beta$を表し、それぞれをマウスかタッチで動かすことができます。

2015-08-30

ミンコフスキーの定理と線形合同法の多次元疎結晶構造

この記事は次の場所へ移動しました。

http://fujidig.github.io/articles/minkowski-and-lcg.html

2015-08-29

R^dのある点列の集積点全体となる集合は？

定義

$\mathbb{R}^d$の点列$\{x_n\}$に対し、この点列の収束する部分列の極限となる点を点列$\{x_n\}$の集積点という。

問題

$\mathbb{R}^d$のある点列の集積点全体となる集合はどんな集合か。

答え

$\mathbb{R}^d$の閉集合である。

必要性の証明

$A \subset \mathbb{R}^d$が点列$\{x_n\}$の集積点全体とする。$A$が閉集合であることを示す。まず、

$a \in A \iff$ 任意の$\epsilon > 0$に対し無限個の自然数$n$が存在して$|x_n - a| < \epsilon$

が成り立つ。

$A$が閉集合であることを示すには$A$の閉包$\bar A$が$A$に含まれることをいえばよい。 $a \in \bar A$, $\epsilon > 0$とする。閉包の定義より$a$の$\epsilon / 2$近傍に$A$の点$b$が存在する。 $b \in A$より無限個の自然数$n$が存在して$|x_n - b| < \epsilon/2$である。すると$|x_n - a| < \epsilon$が無限個の$n$で成立するので$a$は$A$に属する。したがって$\bar{A} \subset A$である。

十分性の証明

$\mathbb{R}^d$の部分集合に対して、「ある点列$\{x_n\}$の集積点全体と一致する」という条件を(P)とする。

証明したいことは任意の閉集合が(P)を満たすことである。

(P)を満たす集合が可算個あったとき、それらの和集合もまた(P)を満たす。実際、(P)を満たす集合$A_n (n = 1, 2, 3, \cdots)$があったとき、各集合に対応する点列をうまく一列に並べればよい。

$\mathbb{R}^d$の閉集合は有界閉集合の可算個の和として書けるので有界閉集合が条件(P)を満たすことを言えばよい。

そこで$A$を$\mathbb{R}^d$の有界閉集合とする。このとき点列$\{x_n\}$が存在して$A$はその集積点全体と一致することを示す。

$\epsilon > 0$とする。このとき $$ A \subset \bigcup_{a \in A} U_\epsilon(a) $$ が成り立つ ($U_\epsilon(a)$は$a$の$\epsilon$近傍)。

$\mathbb{R}^d$の有界閉集合$A$はコンパクトなので、有限個の点$a_1, \cdots, a_n \in A$が存在して $$ A \subset \bigcup_{k=1}^n U_\epsilon(a_k) $$ となる。

正整数$m $に対して$\epsilon = 1/m $として上の方法で得られる$A$の有限列$\{a_1, \cdots, a_n\}$を各$m $に対して選び$S_m $とする。すると$A$の任意の点は有限列$S_m $の中のどれかの点との距離が$1/m $未満となる。

有限列$S_1, S_2, S_3, \cdots$を順につなげてできる点列を$\{x_n\}$とする。このとき点列$\{x_n\}$の集積点全体は$A$となる。

実際、$x_n \in A (n \in \mathbb{N})$で$A$は閉集合だから、$\{x_n\}$のどんな収束する部分列の極限も$A$に属する。

逆に任意の$a \in A$に対して$a$は$\{x_n\}$の集積点である。実際、各$m \in \mathbb{N}$に対して有限列$S_m $の要素で$a$にもっとも近いものを$y_m $として点列$\{y_m\}$をとればよい。 $\{y_m\}$は$\{x_n\}$の部分列であり、$|y_m - a| < 1/m (m = 1,2,3,\cdots)$なので$\lim_{m \to \infty} y_m = a$である。

(証明終わり)

理科